Customizable Stochastic Processes

Markets jump. Volatility clusters. Events create gaps. Traditional models don’t capture these — but ours can. Build and calibrate sophisticated stochastic processes that reflect how markets actually behave, and use them to reveal hidden trading opportunities or build better risk models.

The result: your edge against the market.

Whole-Surface Consistency Reveals Mispricing

Because stochastic process models generate the entire volatility surface from one coherent set of dynamics, any market quote that doesn’t fit the model’s unified structure becomes immediately visible.

This makes it straightforward to spot skew mispricings and cross-expiry inconsistencies that ad-hoc implied-vol fitting methods overlook.

Idiosyncrasy-Free Volatility Surface Leads to Better Forecasting

By modeling the full volatility dynamics, stochastic process models separate idiosyncratic events from true systematic movements. This separation produces cleaner surfaces and enables more meaningful cross-sectional comparisons across different underlyings.

With a cleaner, model-driven surface, quant researchers gain stronger vol forecasting power, more reliable cross-sectional insights, and clearer relative-value signals.

Generate More Reliable Risk Measures

By simulating the underlying dynamics directly, stochastic process models produce sensitivities that reflect real-world dynamics. These models also account for the full dynamics of the volatility surface. They provide a unified foundation for risk management. The same engine that generates market-consistent Delta, Gamma, Vanna, and Volga can produce more realistic scenario paths, stress tests and simulations giving risk managers a coherent view of exposures.

Market-aligned risk measures and Greeks provide clearer insights, allowing for more effective hedging and confident portfolio management.

A Real-World Example

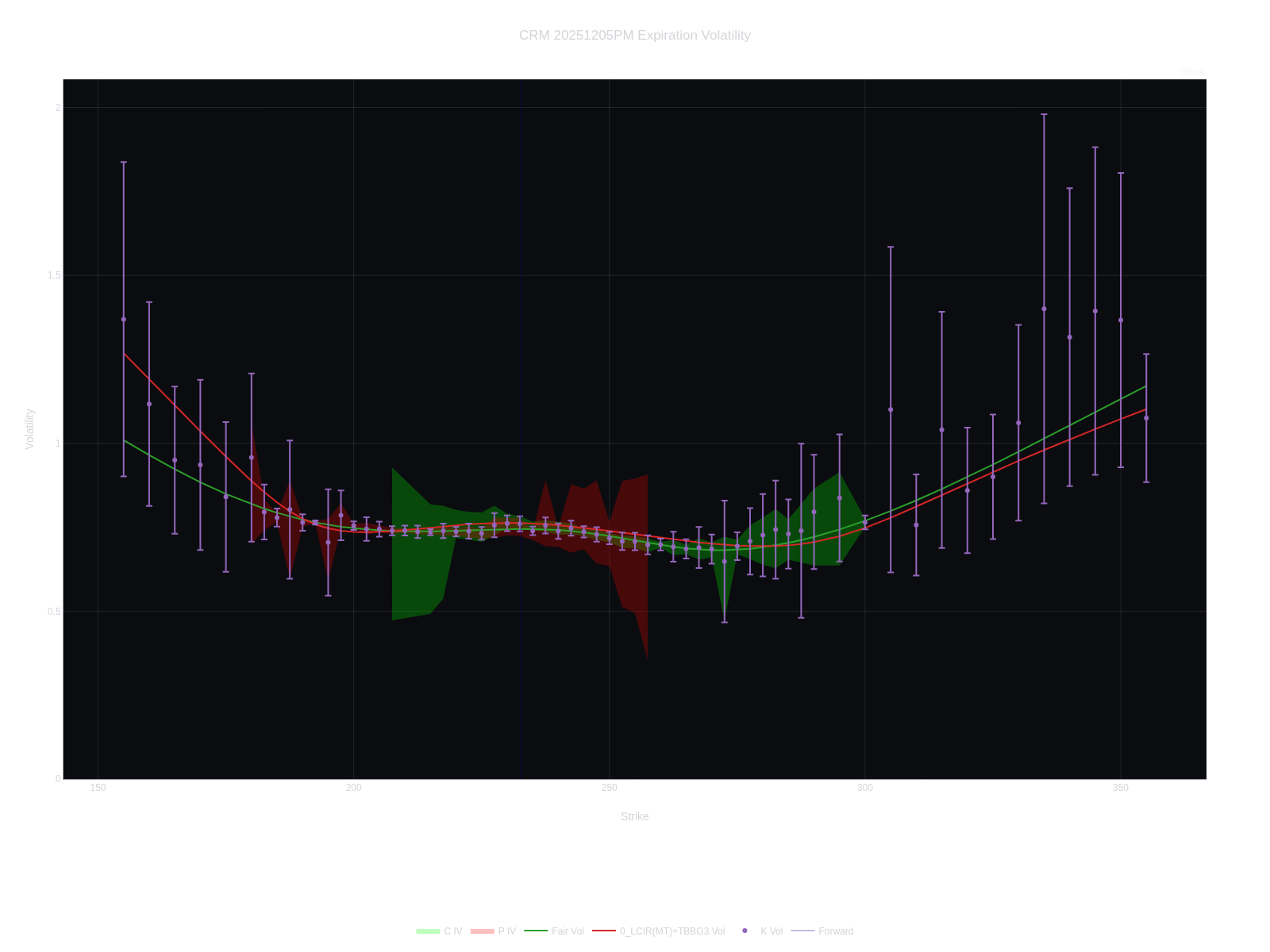
On December 1, 2025, Salesforce Inc. (CRM) was scheduled to report earnings after the market close on December 3—just two days later. The volatility smile for the December 5 expiration clearly reflects this upcoming event: it exhibits a distinct “W” shape, signaling a bimodal Gaussian distribution in expected price returns. This pattern arises because the market is pricing in two materially different scenarios for the post-earnings move.

A stochastic process combining Merton jumps with a leveraged Cox–Ingersoll–Ross (CIR) stochastic volatility component—further augmented by a bimodal Gaussian jump to represent the earnings event—successfully captures both the underlying stock dynamics and the discrete uncertainty introduced by the announcement.

Try It Instantly — No Installation Required

Build your own stochastic process by combining Brownian motion diffusion, Merton, Variance Gamma, CGMY, and Kou jumps, and adding a stochastic time change using Cox–Ingersoll–Ross, Gamma, Inverse Gaussian processes, or others. Calibrate your custom model to the full option chain, then generate Greeks, detect surface inconsistencies, and identify relative-value opportunities — all from a single platform.

A unified foundation for pricing, hedging, risk management, and volatility forecasting. Try it here.